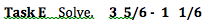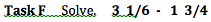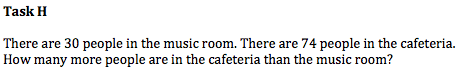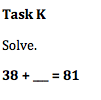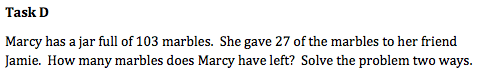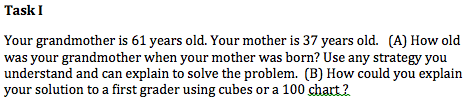Examples of Sorted Tasks
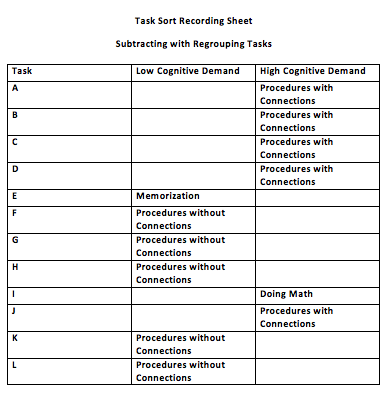
The following is a set of tasks that have been sorted along with an explanation as to why the tasks were sorted in this way. Below is a document that contains all of the tasks that will be discussed within this section. Next is a chart showing how the tasks were sorted. Following, is the explanation of why they were sorted in that manner along with the tasks below.
| subtraction_tasks.doc | |
| File Size: | 2010 kb |
| File Type: | doc |
Memorization:
Memorization tasks are simple tasks that require some of the lowest cognitive thinking that exists. When students memorize, they are simply storing answers in their brains and mindlessly repeating them when prompted. Memorization tasks can also include memorizing rules that are used in solving a problem, such as “PEMDAS.” When students perform memorization tasks, they are not making any mathematical connections or deepening their understanding, but instead, simply spouting out answers that they have memorized. These types of questions are not very helpful unless they are concepts or facts that must be learned by memorization. Task E is can simply be completed through simple math facts that would most likely have been practiced numerous times within the classroom. This task requires no level of higher thinking and can almost be completed "thoughtlessly".
Memorization tasks are simple tasks that require some of the lowest cognitive thinking that exists. When students memorize, they are simply storing answers in their brains and mindlessly repeating them when prompted. Memorization tasks can also include memorizing rules that are used in solving a problem, such as “PEMDAS.” When students perform memorization tasks, they are not making any mathematical connections or deepening their understanding, but instead, simply spouting out answers that they have memorized. These types of questions are not very helpful unless they are concepts or facts that must be learned by memorization. Task E is can simply be completed through simple math facts that would most likely have been practiced numerous times within the classroom. This task requires no level of higher thinking and can almost be completed "thoughtlessly".
Procedures Without Connections:
Tasks that were put into the “Procedures without Connections” category are tasks that require students to use low cognitive thinking and have little understanding of the mathematics behind the tasks. These tasks involve the use of algorithm or demand that a student uses an algorithm that they have been taught. There is little room for creativity in these problems because the students do not make any connections with the math. When completing “Procedures without Connections” tasks, students simply plug numbers into an algorithm mindlessly and follow the steps they were taught to take to find an answer. Task F is in this category because the students do a simple algorithm, learned in class to change the denominator in order to solve the problem.
Tasks that were put into the “Procedures without Connections” category are tasks that require students to use low cognitive thinking and have little understanding of the mathematics behind the tasks. These tasks involve the use of algorithm or demand that a student uses an algorithm that they have been taught. There is little room for creativity in these problems because the students do not make any connections with the math. When completing “Procedures without Connections” tasks, students simply plug numbers into an algorithm mindlessly and follow the steps they were taught to take to find an answer. Task F is in this category because the students do a simple algorithm, learned in class to change the denominator in order to solve the problem.
Procedures With Connections:
We sorted items in the category “Procedures With Connections” because these tasks required students to analyze problems and determine how to solve it. These tasks often require the use of a traditional algorithm; however, the students are not mindlessly performing these algorithms like they would in the low demand tasks. Students are asked to perform tasks that require representing the problem or answer in multiple ways. This could mean using different types of manipulatives or visual representations to do so. Students are also asked to make connections between the different representations to make sure that the students understand the problem and the algorithm that they perform. Task A was put in this category because it does require a higher level of thinking when the students think of a real-life situation, however they are still carrying the standard algorithm. While students are allowed to be creative it is still limited within this task.
We sorted items in the category “Procedures With Connections” because these tasks required students to analyze problems and determine how to solve it. These tasks often require the use of a traditional algorithm; however, the students are not mindlessly performing these algorithms like they would in the low demand tasks. Students are asked to perform tasks that require representing the problem or answer in multiple ways. This could mean using different types of manipulatives or visual representations to do so. Students are also asked to make connections between the different representations to make sure that the students understand the problem and the algorithm that they perform. Task A was put in this category because it does require a higher level of thinking when the students think of a real-life situation, however they are still carrying the standard algorithm. While students are allowed to be creative it is still limited within this task.
Doing Math:
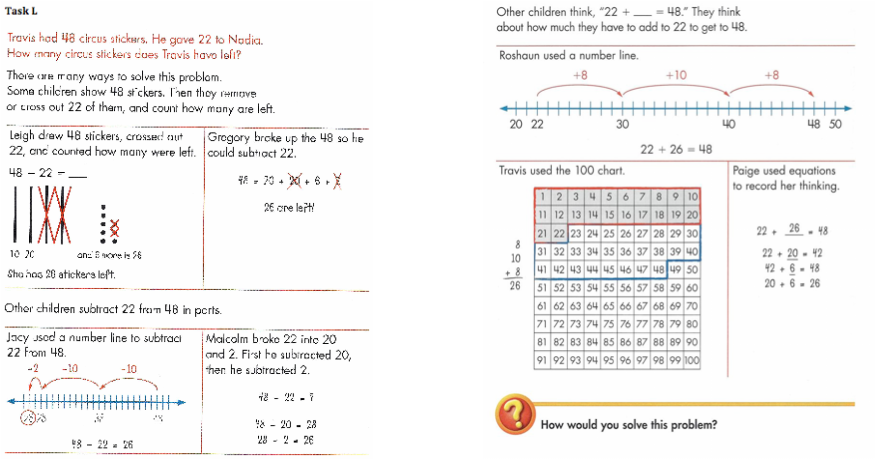
Tasks that were placed in the “Doing Math” category are the most difficult tasks for students to perform. These tasks were placed in this category because they ask students to do advanced math that does not require an algorithm at all. There is no “right” way of doing these problems, and students are able to have creativity in most of their answers. These tasks also require students to self-assess themselves and often they are asked to “explain their answer.” By having students explain what they have done, they must fully understand the math behind the problem. Students are also asked to look at another student’s work and explain their thinking. This is extremely hard for some students because it requires full understanding of the math behind it. Not all students approach problems the same way and if a student is supposed to understand another student’s work that was done a different way than they would have done it, the problem becomes very difficult. Doing math problems often ask students to find relationships between different mathematics, such as subtraction and addition, for example. This also tests students understanding of the math concepts. These are the best types of questions and teachers should strive to make sure that all of their students are able to answer these types of questions. Task I was placed in this category because it allowed students to use anything they understood to solve the problem but also required them to explain the answer through a manipulative.
Tasks that were placed in the “Doing Math” category are the most difficult tasks for students to perform. These tasks were placed in this category because they ask students to do advanced math that does not require an algorithm at all. There is no “right” way of doing these problems, and students are able to have creativity in most of their answers. These tasks also require students to self-assess themselves and often they are asked to “explain their answer.” By having students explain what they have done, they must fully understand the math behind the problem. Students are also asked to look at another student’s work and explain their thinking. This is extremely hard for some students because it requires full understanding of the math behind it. Not all students approach problems the same way and if a student is supposed to understand another student’s work that was done a different way than they would have done it, the problem becomes very difficult. Doing math problems often ask students to find relationships between different mathematics, such as subtraction and addition, for example. This also tests students understanding of the math concepts. These are the best types of questions and teachers should strive to make sure that all of their students are able to answer these types of questions. Task I was placed in this category because it allowed students to use anything they understood to solve the problem but also required them to explain the answer through a manipulative.